 THE DIGITAL
THE DIGITAL
TRANSFORMATION
COMPANY
LITS ADVENTURES supports his clients in creating, implementing and operating their ebusiness and ecommerce strategies
 LITS ADVENTURES
LITS ADVENTURES
LITS ADVENTURES is an ecosystem of companies that supports its clients and society in facing the present and future challenges.
Digital transformation? Yes, sounds great but it’s only a part of it. Digital is already part of everything, so for companies to be able to be competitive they have to transform more deeply. And how can you create digital transformation on a company without understanding its full specificities?
We understand digital well, we understand business well, and we can learn fast about your company so that we can bring all these components together and provide you the right solution for your company.
To achieve this goal, we developed expert solutions for the different components that are essential to digital transformation needs with 3 separate companies that wotk together (we even share the same building).
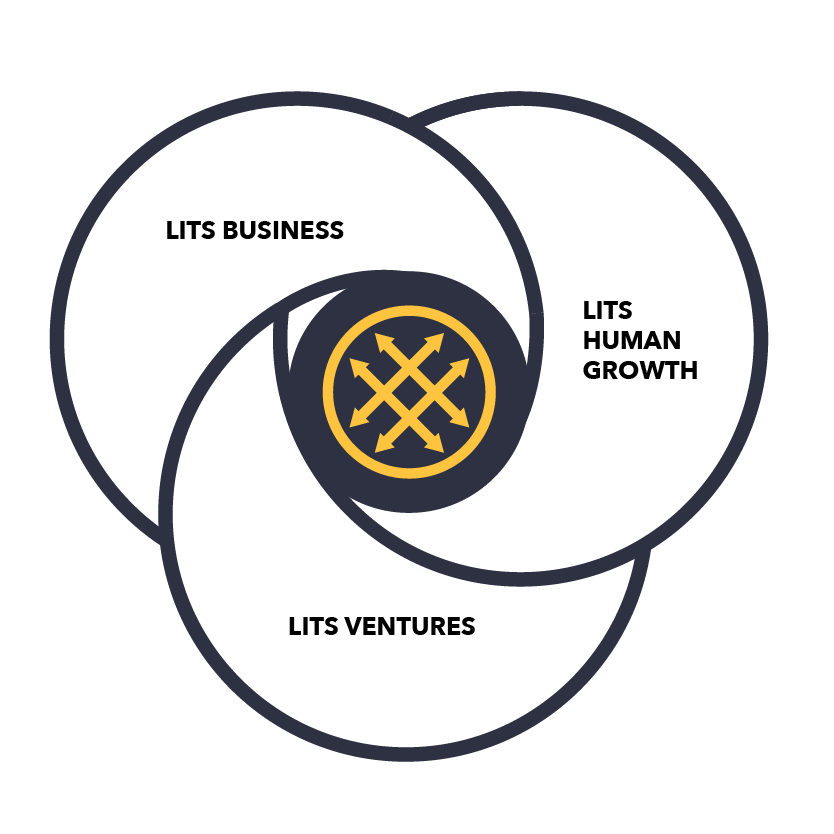
LITS BUSINESS
Transforming companies
Helps companies creating, implementing and operating their digital/hybrid strategies.
LITS HUMAN GROWTH
Transforming people
Of people for digital transformation and the challenges ahead. Through its school (LITS Academy), Media and Blog, and the experience of LITS horses.
LITS VENTURES
Transforming industries
Incubator and company builder where we invest and support the growth of companies we believe in.
 SOME CLIENTS WE WORK WITH
SOME CLIENTS WE WORK WITH
We have the pleasure to work with some of the top companies in Europe and North and South America with a wide range of services, from strategy to omnichannel and digital transformation.

























